
Category: Shapes & Spaces and 3D Objects & 2D Shapes
Suitable for Grade Level: Secondary
The Math in this Problem:
In this puzzle, we explore the world of 2-dimensional geometry by constructing and analyzing shapes, such as pentagons, triangles, and squares. It introduces us to the preliminary notions of optimization, where we work with maximizing and minimizing shapes and spaces.
Understanding such a problem gives us a solid basis for working with and calculating areas of 2-D shapes and eventually, volumes of 3-D objects.
Angela the amoeba, in contemplating the meaning of her life, decided that it was to find a shape for which no regular pentagon existed whose corners touched her outline. For example, this shape didn’t work…

…because a regular pentagon exists whose corners all touch her outline:

Can Angela the Amoeba satisfy her meaning of life?
Extensions:
After attaining her meaning of life, Angela the Amoeba decided she needed something new and far more challenging. She decided to find a shape for which no equilateral triangle could be found whose vertices all lay on her outline. Prove that no matter how hard Angela tries, she can never find such a shape.
Angela eventually gave up with the triangle and started to pursue an even higher meaning of life. This was to find a shape for which no square existed whose corners touched her outline.

…because a square exists whose corners all touch her outline:
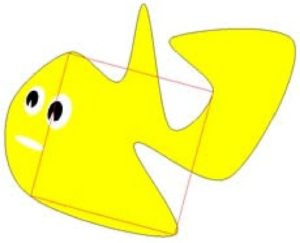
Can Angela the Amoeba satisfy her higher meaning of life? Warning: This is an unsolved problem in mathematics.
The Extension is a classic problem.
