Math Fair Problems

In this puzzle, we explore the world of 2-dimensional geometry by constructing and analyzing shapes, such as pentagons, triangles, and squares. It introduces us to the preliminary notions of optimization, where we work with maximizing and minimizing shapes and spaces.

Understanding such a problem gives us a solid basis for working with and calculating areas of 2-D shapes and eventually, volumes of 3-D objects.

A polyomino is a geometric shape, made from any number of squares joined by their edges. In this investigation, we work with pentominoes, five squares, and triominoes, 3 squares, where we study the unique shapes from constructing them in all different ways. Students can observe and comprehend the concepts of reflections and rotations by manipulating the various polyominoes.

This investigation introduces the mathematical operation of exponentiation, which is essentially repeated multiplication. This puzzle specifically explores the powers of two, which are often used to measure computer memory and thus, have become consistently apparent in computer software. Exponentiation is also commonly and frequently used in within natural sciences, where we work with population growth.

This problem explores the geometric world of working with coordinates, formulating linear equations using these coordinates, and solving for points on the graph given these equations. In this puzzle, students are given a fun scenario dealing with finding out where a pirate’s treasure has been buried. They will develop a basic understanding of applied mathematics and discover that these fundamental principles are applicable to real-life situations.

Within the realm of statistics, there are key concepts such as data sets, samples, and averages, which are most commonly calculated by finding the mean. Setting an emphasis on analysis, students are asked to carry out an experiment by constructing a unique set of data using dice then finding out the average using the numbers within their sample. This gives them a general understanding of statistics as later on it becomes more complex, including concepts such as variance, standard deviation, and distributions.

This investigation studies probability theory, which is used to draw conclusions about the likelihood of potential events through quantitative analysis. Students will apply the binomial distribution probability mass function, which generates the probability of successes in a trial, given a known probability value and number of independent experiments. After gaining an understanding of this simple distribution, students will better transition to other more intricate probability distributions.

In this puzzle, students are presented with a math problem in the form of politics, where two parties are attempting to win over votes from various districts, with each district representing a different number of votes. The use of analytical skills and mathematical operations, such as addition and subtraction, will be particularly useful when progressing through this brainteaser.

The most commonly used example in investigating probability theory is rolling dice. Through playing this simple game, students will observe laws of probability, such as each roll being random and independent from any other roll, the consistency of the probability of each value on the die being rolled, and tabulating the complement of an event by figuring out the probability that this event will not occur.

In this math puzzle, students will analyze various shapes, while applying them to simple designs within urban planning. The simplicity of road planning within this investigation will give a general idea of the importance of shapes and their use in practical applications.

In this investigation, students will be introduced to the fundamental principles of modular arithmetic, which involves working with a system of mathematical operations. Using addition and subtraction, along with division and remainders, this problem is a simple investigation for gaining an understanding of how combining operations can solve various problems.

Colouring is a profound mathematical topic with many industrial applications. This math puzzle involves strategic planning in the process of colouring maps. Given a specified number of colours, students are challenged with the constraint of regions sharing an edge not being filled with the same colour. Progressing through this brainteaser, students find themselves tackling the same problem that many mathematicians currently face.

In this investigation, students will work with different colours and shapes, having to discover the various arrangements, and whether or not some even exist. This conundrum involves analytical processing and mathematical logic, leading the kids to an introduction to mathematics and its relationship with shapes, colours, and arrangements.

In this puzzle, students will gain an understanding of circuit boards and their well-designed structure to prevent the use, and its messy arrangement, of wires. Given certain constraints, puzzle-solvers will need to figure out a way to structure a circuit board so that connections can be made successfully.

This classic problem has students working with a variety of polyominoes, studying their properties while performing all sorts of rotations with them. By studying these unique shapes, students can observe and comprehend the concepts of reflections and rotations by manipulating these various geometric forms.

This brain teaser involves experimenting with measurements and various containers. Students will work on problem-solving skills, using simple arithmetic operations (addition and subtraction) to derive at solutions for this investigation.

In this puzzle, the students work with single digits and are given the task of placing them in different shapes and patterns. Given procedural constraints, such as not permitting certain digit placements, this problem allows the kids to utilize and build on their analytical and problem-solving skills.

Playing cards can help kids learn number sense and practice mathematical operations. Using an ordinary deck of playing cards, Double Dozen challenges students with a math game that deals with multiplying, dividing, adding, and subtracting various card values to equal a given number.

In this investigation, students will observe statistical trends and patterns from the provided data. Using the given information, mathematical analysis can be executed, chiefly studying the relationships, correlations, and dependence evident in this statistics-related puzzle.

Egyptian Fractions are unique because they only possess numerators equaling 1. In this brainteaser, students will manipulate fractions in order to create a summation of Egyptian Fractions, starting with the largest possible term and ending with the smallest possible term.

Operations Research is a branch in mathematics, which uses skilled methods to obtain optimal decisions to problems. These include those concerned with minimizing costs or maximizing profits, which are also correlated with amount of time research takes.  In this investigation, students are presented with the challenge of strategic planning and carefully allotting the time it takes to thoroughly complete a research project.

This puzzle introduces the use of an abacus, which is a mechanical device that temporarily stores numbers during a mental calculation. With the use of such a tool, students will be able to make computations using different mathematical operations, including the conversion of numbers with different bases, but mainly studying the properties of factorials.

In this math puzzle, students will experiment with playing cards and be introduced to the idea of cryptography, which is the practice of hiding information through secret codes. It is related to disciplines, such as mathematics, computer science, and engineering, and is the foundation for building applications, including computer passwords and debit cards.

This brainteaser involves observing the composition of structures and discovering similarities among these various arrangements. Incorporating such a task into a fun and competitive game will surface enthusiasm out of the students in learning about different structural properties and relationships, which is an important introductory topic to applied mathematics.

Game theory is a form of mathematics, which attempts to predict behaviour in any sort of strategic setting. This puzzle involves careful tactical patterns and analytical processing in order to master this math challenge. Similar to other strategy-based games, Frog Catchers is concerned with the evaluation of setting up goals and future play possibilities of one’s opponent.

In this math puzzle, students are investigating different number values assigned to frogs and their placements on lily pads in a game of hopscotch. With the goal of correctly placing the frogs on certain lily pads to have them never land on the same one, students will practice mathematical analysis in examining the various arrangements.

Through the development of geometric concepts, including dimension and space, mathematicians began to study topology, a major area involving spatial properties of objects. This math puzzle involves careful, strategic planning and mathematical reasoning in order to derive a suitable solution to this maze-related conundrum.

This problem belongs to the branch of mathematics called Graph Theory. A graph bears no relation to the graphs that chart data, such as the progress of the stock market or the growing population of the planet. And you are correct, Euler was the mathematician who created this branch of mathematics. It arose from a famous problem he was working on called the Bridges of Konigsberg. Take a look at the abstract rendition of the Bridges of Konigsberg Problem to determine how to abstract the mathematical interpretation of the real situation.

In this math puzzle, students experiment with shapes, particularly triangles and hexagons, creating different patterns involving these two forms. Examining the respective attributes to each shape, students are challenged to build various patterns based on the unique elements possessed by triangles and hexagons.

This investigation involves analytical reasoning in order to predict future occurrences. In this puzzle, students will develop and apply various strategies to develop a fitting solution.

This math puzzle was inspired by the stacking game DVONN, in which the objective is to accumulate pieces in stacks. Similarly, Grasshopper Jump Fest requires students to apply abstract strategy in order to develop the required grasshopper-stacking solutions.

Use patterns to describe the world and to solve problems. Describe and compare everyday phenomena, using either direct or indirect measurement. Describe the characteristics of 3-D objects and 2-D shapes, and analyze the relationships among them. Perform, analyze and create transformations.

In this investigation, students are challenged to combine research analysis along with mathematical statistics to arrive at an appropriate solution to this extraterrestrial civilization problem.

This investigation introduces students to the fundamental principles of modular arithmetic. Working with a system of mathematical operations, including addition and subtraction, along with division and remainders, this math puzzle allows students to gain an understanding of how combining arithmetic operations can solve various problems.

This math puzzle explores lines and angles, while working with different two-dimensional shapes and patterns. Students will incorporate their understanding of lines and angles with the practical application of experimenting with the effectiveness of lights in various surroundings.

In this investigation, students will use strategic thinking to develop a well-sought answer. Integrating the probability notion of randomness, this experiment will allow for students to search for strategic and reasonable predictions in order to come up with a precise solution.

Injection molding is a technique for constructing plastic objects, including toothbrushes, hair combs, buttons, and food containers. This math puzzle introduces students to the concept of injection molding and its relationship with mathematics, as it pertains to the complex geometry of creating various products with different shapes and sizes.

In this math puzzle, students will experiment with number sequences and patterns, using single digits. More particularly, arithmetic sequences are the number patterns investigated here. Students will gain an understanding of common number patterns and a foundation for branching off to more complicated, related topics, such as geometric and special sequences.

In this investigation, students are introduced to the Fibonacci sequence, more specifically as it is evident through the recurrence relation defined by triangular patterns. This coin-related puzzle will provide students with an idea of the patterns and sequences aspects within mathematics.

Given rules and restrictions like many other board games, this math puzzle challenges students to experiment with various strategies and tactics to reach the main objective: to help Jason defeat the dragon-tooth-warriors.

This math puzzle presents students with the problem of orders and combinations, which are fundamental principles in the realm of probability and statistics. Developing an understanding of this simple conundrum will serve as an introduction to these extensive areas of mathematics.

Mathematics is sometimes viewed as the science of patterns, which can be spatial, temporal, or sequential. Through applying strategies and analytical reasoning, Jumping Chips presents students with the challenge of recognizing patterns using chips and even themselves!

This puzzle challenges students to observe and analyze shapes, along with their respective dimensions and measurements. Using patterns found in real-life objects, particularly those used to form bricks and solid metal pipes, students will simulate constructing such items using triangles and rectangles.

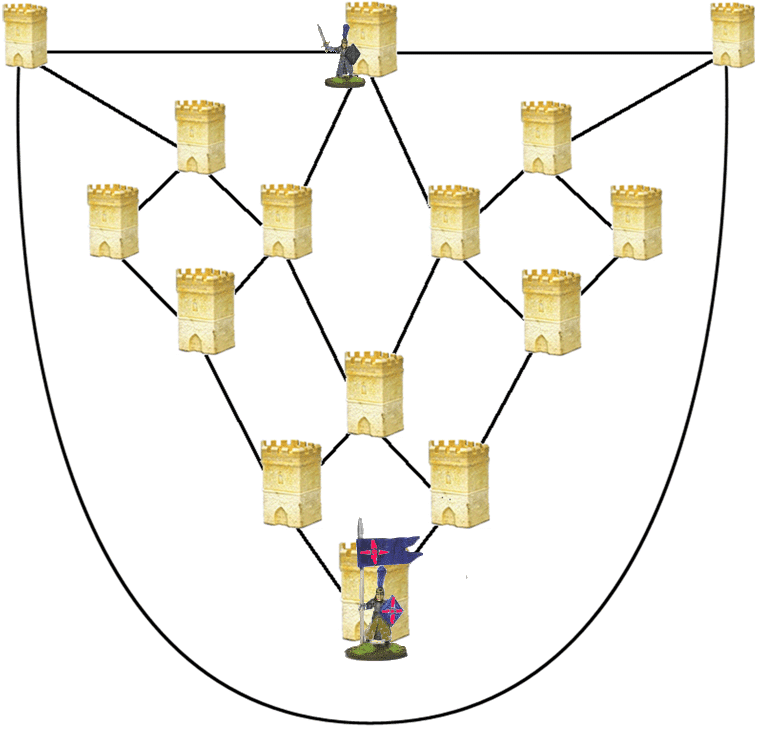Students will practice strategic analysis while arriving at solutions for how many moves each knight must take in order to catch the other. This investigation is associated with basic game theory, which is a branch of mathematics attempting to capture behaviour in strategic situations.

Dans ce casse-tête mathématique, les élèves expérimenteront des séquences de nombres et des modèles en utilisant des chiffres uniques. Plus particulièrement, les séquences arithmétiques sont les modèles de nombres étudiés ici. Les étudiants acquerront une compréhension des régularités numériques courantes et une base pour passer à des sujets plus complexes et connexes, tels que les séquences géométriques et spéciales.

Students will study a variety of circles with different on-off configurations in order to arrive at solutions for turning all of the light bulbs on. This investigation involves strategic analysis and mathematical reasoning of various arrangements of lit and unlit light bulbs.

Click here for an online version of this problem, thanks to Dr. Paulino Preciado Babb.  

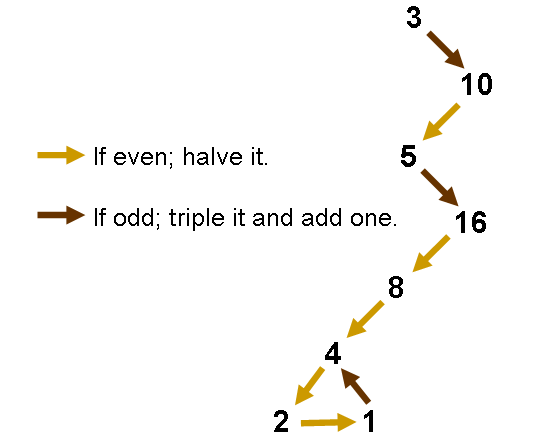In this puzzle, students are presented with number patterns that are formed by carrying out specified mathematical operations, depending on the values presented. Working with these various patterns, students will study their respective properties and whether or not all number sequences end in the value 1.

This logic puzzle involves studying the various arrangements of correctly-labelled and mislabelled pasta sacks. Progressing through this brainteaser will provide students with an understanding of permutations, which is an area of mathematics associated with the rearrangement of multiple objects or values.

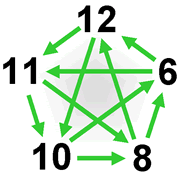This math puzzle involves the construction and comparison of various number sequences. Progressing through this investigation will help students understand the relationship between these simple sequences and their respective linear equations, which they will learn can be used to solve a variety of useful problems.

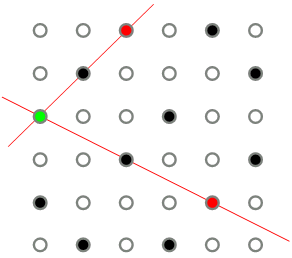In this classic problem, students are presented with a puzzle involving arrangements and angles within various squares. This investigation simulates the practical application of viewing all minarets from every other one in the utopian downtown of New Istanbul. The objective of this puzzle is for students to come up with suitable arrangements so that all positions representing minarets could be connected to all other ones using a straight line.

Using digits 1 through 4, Mini Sudoku serves as a simplified version to the classic Sudoku game to be solved in math fairs. Progressing through these math puzzles will require students to practice mathematical analysis, focusing on counting possible solutions given initial values presented on the grid.

T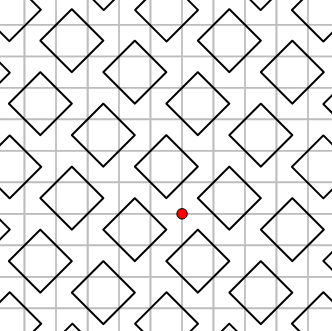his math puzzle challenges students to work with light beams reflected off mirrors within various boxes. To simplify the notion of reflection, which is a fundamental notion of mathematics, this brainteaser introduces it using 90 degree angles.

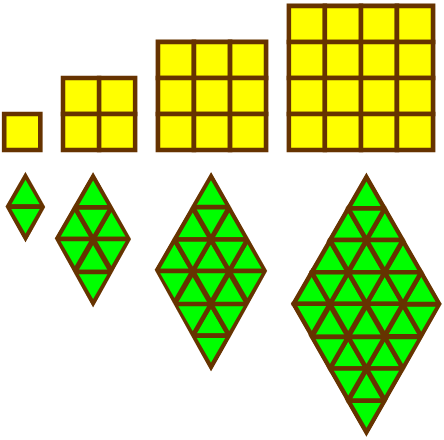In this investigation, students are introduced to shapes and designs used within housing designs and blueprints. Applying the idea of convexity, which helps with heat conservation, students will experiment with constructing various complexes using 7 to 12 sides.

This math puzzle presents the challenge of creating various paths from one point to another. Students are given this brainteaser that involves figuring out unique solutions that will connect points representing Mongol Men and Mongol Maidens’ tents. Through performing grid analysis, the desired routes necessary to join the corresponding colours will be achieved.

This math fair game engages students in a game like bingo, where they randomly assign numbers (1-100) to their grid and use two 10-sided dice to call out numbers. The objective of such a game is to observe and study the outcomes from multiplying the rolls from the two dice. The mathematics and observations associated with Multipingo are fundamental lessons in probability.

This math problem involves directions, probability, and shapes. Similar to hopscotch, the goal is to go over all areas of the shape. Students must use analytical reasoning to figure out whether or not the goal in obtainable starting from all different spots and if not, which spots allow for such a goal to be achieved.

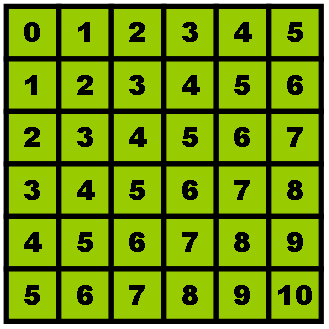In this investigation, students will perform various mathematical operations to discover patterns within numerically-ordered squares. This exercise will serve as an introduction to understanding mathematical pattern analysis, which is widely used when making educated guesses.

This exercise involves mathematical pattern analysis of a long row of alphabets. Using the same line, students are challenged to show that there are ten consecutive sequences without a sequence following an identical one.

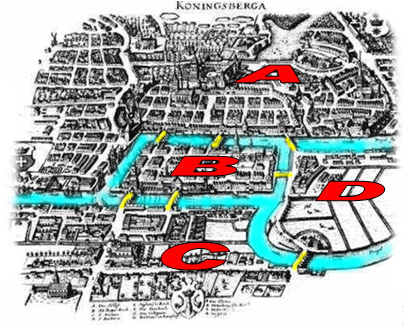This is a classic problem, also known as the Seven Bridges of Kӧnigsberg, which was solved by Leonhard Euler, one of the greatest mathematicians. Party in Kӧnigsberg challenges students to analyze the vertices, edges, and faces of proposed surfaces and derive a solution to this topology problem similar to that of the Euler characteristic.

This brainteaser involves the analysis of lines, dimensions, and shapes. Using the knowledge they have of these fundamental notions of mathematics, students are faced with a problem involving patterns and deriving formulas to representing such patterns.

Progress Reaches Asteroid is a challenging puzzle that involves the analysis of direction and similar elements to that of a Rubik’s cube. In order to find suitable starting points so that none of the four pieces placed on the asteroid will ever meet on single square, students will have to apply strategic analysis when formulating a solution for this problem.

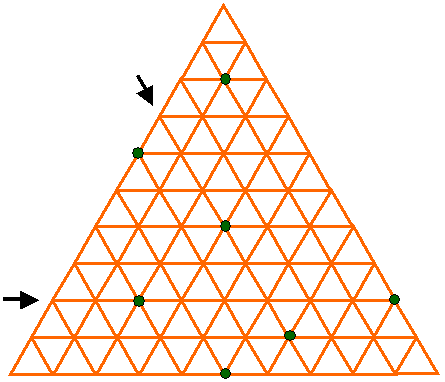This math problem challenges students to analyze and study the properties of a triangular chess board. With the constraint of not allowing two Queens to be on the same line, students will come up with the many ways of placing 7 Queens on various intersections. They are also challenged to place 6 Queens in a certain way to refrain from allowing a 7^th to enter the chess board.

In this investigation, students will analyze squares of various sizes. Each square must be transformed into a different one, while the goal is to move the least number of units possible. By progressing through Quilt Mending, students will be engaging in the notions of efficiency and productivity, which are assets in our economy.

This math puzzle involves the detailed investigation of squares and its properties. Students are challenged to build squares made up of smaller squares. Using the knowledge they have of shapes, various observations will be noted, including which scenarios are impossible to create.

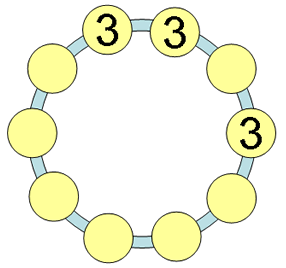Ring of Threes is a math investigation involving the application of multiplication and addition with single digits. Students will have to analyze various number sequences, while applying these basic mathematical operations.

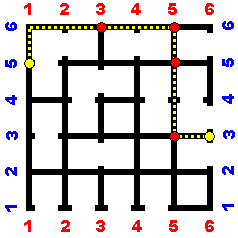In this brainteaser, students will analyze and create various-sized grids. Since traveling from block to block takes one second and crossing an intersection takes an extra second, students are challenged to build efficient grids that only take a maximum of a specified number of seconds.

Vectors are the basis to this math puzzle, where students will apply their knowledge of directions and lengths onto a grid. With the acceleration of each consecutive vector, students are challenged to derive a solution for finding a way back to the coyote’s initial position.

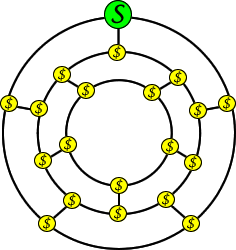This math problem was invented by the great Irish mathematician, William Rowan Hamilton. In this Icosian game, the goal for students is to find a path such that every point is visited a single time and the ending point is the same as the starting point. This path is also known as the Hamiltonian cycle along the edges of a dodecahedron.

Siege Geometry is an investigation associated with angles, shapes, and area. Applying these notions to a case involving cannons and fortresses, students will be able to relate mathematics to a very practical and valuable application used in combat.

Snake in a Box requires two players to participate in this board game, in which one is a cobra player and the other is a snake charmer. One goal of this puzzle is to exercise strategic placement of the numbers 1-25 on a 5×5 grid to make it difficult to figure out how the cobra is wrapped up. Meanwhile, the snake charmer applies strategic analysis in order to take as little number clues as possible to find out how his opponent has curled up the cobra.

Snazzy Triangle is a simple test on the basic understanding of arithmetic operations. In this investigation, students will work with the numbers 1 through 6 and arrange them on a 6-unit triangle. The order of these numbers will have to be precise so that the sums of each side are equivalent to the numbers that students are presented with.

Related to the Fibonacci sequence of multiplying rabbits, this math puzzle introduces students to a simple finite series involving the powers of two, which can be calculated by finding the sum of the terms in the sequence. Snow Day Phone Chain will present students with the total number of terms, which will be used to formulate sequences and to figure out their respective summations.

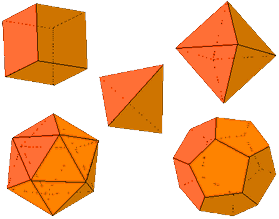This math investigation revolves around the functionality of LCD numbers that we see on a stair climber, microwave, or alarm clock. Students will be challenged to note the number of changes in a complete cycle of numbers, as well as figure out which cycle of numbers would require the least number of changes.

Every student goes through school constructing 3D shapes out of paper, using outlines that are provided by their teachers. However, in this math puzzle, the challenge is to analyze the structures of various Platonic solids and correctly place the tabs along their successive edges.

A sword of knowledge can slay the Dragon of Ignorance, who has three heads and three tails. With one stroke, slayers can chop off one head, two heads, one tail, or two tails; however, the consequences lead to a variant of the structure. In order to successively slay the Dragon of Ignorance, Students must exercise strategic analysis when fighting this creature.

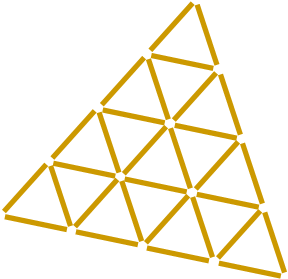This math investigation is associated with shapes, with a great emphasis on triangles. Puzzlers are presented with a huge triangle filled with smaller, identical ones. By experimenting with this shape, students must analyze its properties and figure out the ways to manipulate the total number of triangles by filling in one or more of the structure’s units.

This puzzle focuses on geometry, more specifically the tetrahedron, which is a polyhedron that is composed of four triangular faces. Using the formula for volume, students are challenged to calculate the height of the newly formed shape when the four tetrahedrons are snuggling.

The corners of a cube are coloured with blue, red, yellow, and green in a certain way so that you cannot be on the same colour moving from one corner to the next. In this investigation, students will use colour-coded cards to produce random sequences that represent the movement from one corner of the cube to another. The objective of this game is to recognize the various patterns using these results.

The goal of this math puzzle is to swap the places of the green frogs with the yellow frogs. Since there are constraints when moving along the Lily pads, students must use strategic analysis when planning out the frog jumps. The goal of this game is to figure out whether or not this is even possible and if it is, they are challenged to formulate a solution to represent this scenario.

There are over thousands of tile patterns to choose from but in this case, the Wise Women of Titan do not want identically shaped rectangles to touch at any point, or two identical triangles to touch along any edge. This math puzzle introduces puzzlers to the world of tiling, and the important role that shapes play in creating tile patterns. Students must apply their knowledge of rectangles and triangles, and analyze these shapes to fulfil the Wise Women’s request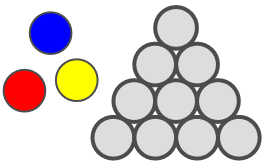s.

Using red, blue, and yellow circles, students are challenged to fill in various shapes made up of circle units. The test of Touching Circles is to not have a circle next to another one of the same colour. Since the different colours can be applied one by one, this makes for a fun two-player game, with the winner being the last one able to make a move.

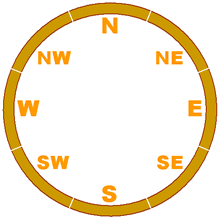In this investigation, students will apply the knowledge they have of direction (north, south, west, east), using a circular track, reflecting a variation of a compass. Given a bit of information about the trains moving along this track, students must figure out the direction in which they are moving, as well as the length of the train.

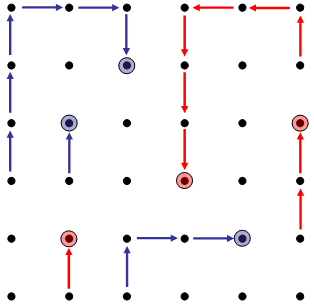In this Tree Planting game, two players will take turns planting their trees and then moving along a grid until one player cannot move onto a dot that has never been occupied before. In order to be successful in Tree Planting, students must be strategic with where they start planting, as well as plan calculated routes to avoid becoming the first player stuck.

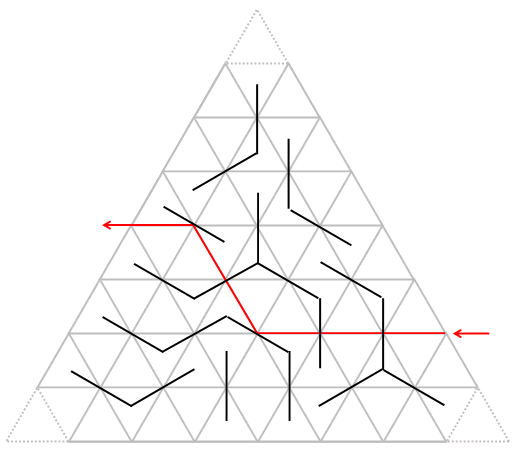This investigation challenges puzzlers to work with light beams that are reflected off mirrors within a triangular box. Using the knowledge they have of geometry and angles, students must execute various routes based on the transformations made by oblique and non-oblique angles.

Twinkle Twinkle is an exploration of astronomy, where we will investigate stars and constellations. Students will make observations about cycles and loops, as well as discover the complexity of space by using mathematics to calculate valences and constellations.

A polyomino is a geometric shape, made from any number of squares joined by their edges. In this puzzle, students experiment with polyominoes of all different sizes. The goal of Un-Babushka Squares is to construct the sizes so that a smaller polyomino cannot fit perfectly inside of another one.

In this math investigation, students are challenged to construct buildings of all different heights, with the floors of all buildings combining to a total of ten floors. Organizing the combinations in a table, students will have to figure out the various ways of doing this, as well as the total number of ways, and evaluate which way(s) actually makes for a good plan.

In this math puzzle, students are presented with King Midas’ gold-filled urns. In order to keep the King from getting bad luck, they must figure out a way to keep the pattern consistent when adding more urns to his collection.

This classroom investigation involves the observation of shapes and colours within a given tile pattern. Having to eliminate two colours, students must study these properties and figure out a way to keep Vermeer’s Paintbrush from resting its ends on tiles of the same colour.

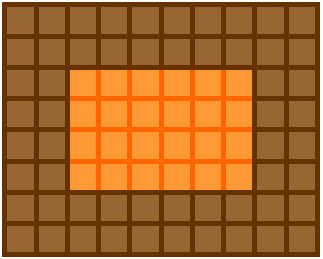The Walls of Rock puzzle proposes the problem of constructing a large castle, including thick walls as well as a big courtyard area. Using the knowledge they have of areas and other mathematical operations, students are challenged to find a way to reconstruct the castle to have the two areas equal, while keeping the thickness of the walls constant.

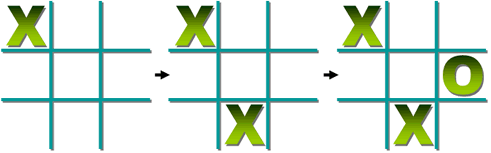This variation of Tic-Tac-Toe allows the players to place either an X or an O onto the 3×3 grid. The winner is the first player to complete three X’s or three O’s in a row. This twist to the game really forces students to analyze the grid and their opponent’s potential moves, having them strategize more than they would have in the original version.

Wolf Nim is structured with pigs lined up beside one another in rows and columns. In this math fair game, students are challenged to strategize a way to have their opponent be the one to eat the last pig. After playing this game with different variations of rows and columns, students are tested to observe the advantages or disadvantages of being the first player to move.

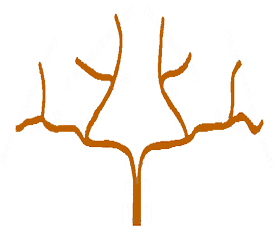This math puzzle introduces us to the Markov Diophantine equation, in which a Markov number is a positive integer x, y, or z that is part of its solution. Experimenting with various numbers, students are challenged to come up with a few of the many triple solutions to this formula, which was named after Russian Mathematician Andrey Markov.

In this math investigation, students will experiment with paper and scissors, cutting out saw-toothed patterns to create paper trees of various sizes. Observing the different shapes that could be created, including the number of branches each possesses, students are tested to construct paper trees that will each hold its respective number of ornaments.