Galileo Educational Network – Inspiring a Passionate Commitment to Learning
Category: 3D Objects & 2D Shapes, Patterns, and Variables & Equations
Suitable for Grade Level: Elementary and Secondary
The Math in this Problem:
In this classic problem, students are presented with a puzzle involving arrangements and angles within various squares. This investigation simulates the practical application of viewing all minarets from every other one in the utopian downtown of New Istanbul. The objective of this puzzle is for students to come up with suitable arrangements so that all positions representing minarets could be connected to all other ones using a straight line.
Minarets in the utopian downtown of New Istanbul will be so beautiful that it will be the law that from every minaret, every other minaret may be seen. When the downtown was small this was relatively easy. The following shows 6 minarets in a downtown of 3×3 blocks:
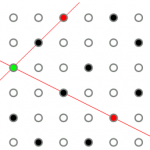
However, it becomes more difficult to construct minarets in a larger downtown. Below a mistake has been made because a person on top of the green minaret cannot see either of the red minarets:
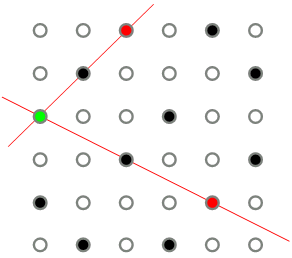
There are two utopian solutions for placing 8 minarets when the downtown grows to 4×4. Can you find both of them?
Extensions:
- What is the maximum number of minarets you can place in an NxN utopian downtown?
- How many minarets can you place in a 5×5 utopian downtown?
- There are two solutions for placing 12 minarets in a 6×6 utopian downtown. Part of each has been completed below:
- There are two ways to build 20 minarets in a 10×10 utopian downtown. Complete the second downtown:
- Is there any limit to the size of a utopian downtown if its NxN blocks must contain 2N minarets?
*Warning: This is an unsolved problem in mathematics.