Galileo Educational Network – Inspiring a Passionate Commitment to Learning
Category: 3D Objects & 2D Shapes and Variables & Equations
Suitable for Grade Level: Elementary and Secondary
The Math in this Problem:
This puzzle focuses on geometry, more specifically the tetrahedron, which is a polyhedron that is composed of four triangular faces. Using the formula for volume, students are challenged to calculate the height of the newly formed shape when the four tetrahedrons are snuggling.
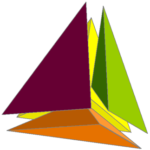
On a cold winter evening, Olive, the green tetrahedron said to her identical quadruplet sisters “It’s so cold that my vertices are numb, my edges are cracking, and my faces are getting frost bite. Why don’t we huddle together and make a giant tetrahedron to keep warm!”
And so they did…
It was a perfect giant tetrahedron, and the best thing about it was that one vertex of each of the four sisters was cozy and warm right in its centre.
“Hey” said Olive, “do you realize that when our giant tetrahedron is lying flat in the snow, that it is exactly 1 cm tall!” I wonder, continued Olive, “When lying flat in the snow, how high are our warm vertices in the centre of our giant tetrahedron?”
The giant tetrahedron performs a pirouette (left) and lies flat in the snow (right).
Hint: The only formula you will need is that the volume of a tetrahedron is one third the area of its base times its height.