Galileo Educational Network – Inspiring a Passionate Commitment to Learning
Category: Number Concepts, Transformations, Number Operations, 3D Objects & 2D Shapes, and Measurements
Suitable for Grade Level: Elementary and Secondary
The Math in this Problem:
This math investigation revolves around the functionality of LCD numbers that we see on a stair climber, microwave, or alarm clock. Students will be challenged to note the number of changes in a complete cycle of numbers, as well as figure out which cycle of numbers would require the least number of changes.
The LCD numbers on a stair climber or alarm clock or microwave are made up of straight sections arranged either horizontally and/or vertically. That is, the number 9 is made up of 6 sections, the number 1 has 2 sections, and the number 4 has 4 sections:
When the numbers are counting down, the numbers change by turning off or on different sections. For instance going from 7 to 6 consists of 5 changes (4 sections turn on and 1 section turns off) and going from 6 to 5 consists of 1 change.
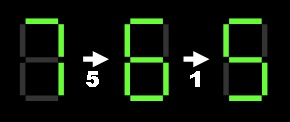
How many changes are there in a complete cycle of the numbers, 0-9-8-7-6-5-4-3-2-1-0?
What order of numbers would involve the least number of changes? You must cycle through all the numbers and back to the first number that you started with.
Game:
- Shuffle a stack of cards with the 10 digits on them. Deal the 10 cards face-down in a circle.
- Players take turns choosing any pair of side by side cards and swapping their position, but they can only do this if the number of changes around the whole circle decreases.
- The person who makes the last swap wins.
Extensions:
- How does the number of changes in the final circle of the game compare to the minimum number of changes?
- What order of numbers involve the greatest number of changes?
- Why is the number of changes between numbers important?