Training Trains

Category: Number Concepts and 3D Objects & 2D Shapes
Suitable for Grade Level: Secondary

The Math in this Problem:

In this investigation, students will apply the knowledge they have of direction (north, south, west, east), using a circular track, reflecting a variation of a compass. Given a bit of information about the trains moving along this track, students must figure out the direction in which they are moving, as well as the length of the train.

When in grade 1, locomotives learn by going round and round in circles on specially created tracks like the one on the right.

The circular tracks are created by combining 8 identical pieces of curved track. In order to remember where they are, the young trains label the tracks:

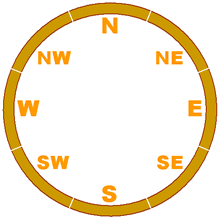
N for North
NW for North-West
W for West
SW for South-West
S for South
SE for South-East
E for East and
NE for North East

They labelled them like this because track N was furthest North, track W was furthest West… You understand the way they were thinking.

To avoid getting confused, the locomotives would chant “North” just as they got to the most northerly part of the circle (in the middle of the piece of track marked “N”), but would remain silent all the rest of the time.

One day, the caboose at the end of one train, realized that whenever its locomotive called out “North”, that was exactly the position that the caboose was moving! Is it possible to tell which direction the train is going round the track? Is it possible to tell the length of the train?

Extensions:

After the young locomotives had graduated from grade 1, they are start grade 2 and are allowed to use up to 16 sections of the curved track (labelled N, NW, W, SW, S, SE, E, or NE) to create more complex loops.
Is there a loop allows the trains to chant “North” five times? (This would mean that 5 of their 16 pieces of track would have to be oriented in the same position as the track marked “N”)
How many different loops are there? (Define what “different” means before you begin.)
By grade 3, the young locomotives are allowed to add one piece of straight track to their loops. How long could this straight piece of track be so that it fits in a loop with the labelled, curved tracks?
In grade 4, the young locomotives are asked to give back their straight bit of track, but they are given “Y-intersections” in return and asked to build the following railroads. Is it possible for a locomotive starting in the middle and pointing Easterly, to travel so that he comes back to the middle, but now faces Westerly?

Design a railroad using the fewest pieces of track
that does not have a dead end and allows a locomotive to change direction.

UnHint

A hint should be helpful! A REAL hint

Find the smallest loop which reverses the direction of the locomotive.
Show that the numbers of E and W curved track must be even (because root 2 is not rational). Do the same for 4 opposite pairs of curved track (N & S, NE & SW, NW & SE). Show that this is impossible.
PS. Don’t be fooled, the diagram above is not correct.

By grade 5, the young locomotives are given as many “Y-intersections” as they want. Then they are told to construct a railroad.
- Is it possible to use exactly 1 Y-intersection?
- Is it possible to use exactly 2 Y-intersection?
- Is it possible to use exactly 3 Y-intersection?
- Is it possible to use exactly 4 Y-intersection?
- Is it possible to use exactly 5 Y-intersection?
- Is it possible to use exactly 6 Y-intersection?
- Is it possible to use exactly 7 Y-intersection?
- Is it possible to use exactly 8 Y-intersection?
- Is it possible to use exactly 9 Y-intersection?
- Is it possible to use exactly 10 Y-intersection?

A Y-intersection is created by overlaying two curved tracks
so, this Y-intersection is a combination of E and NW curves.