Factorial Abacus

This problem is best for people who can express numbers in different bases.

An abacus is a mechanical device for temporarily storing numbers during a mental calculation. An abacus consists of beads that can slide back and forth on rods with each rod being associated with a value.

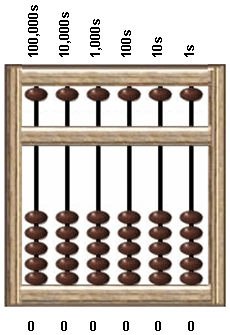
A base 7 abacus helps store keepers keep track of numbers in base 7. A typical base 7 abacus looks like this:

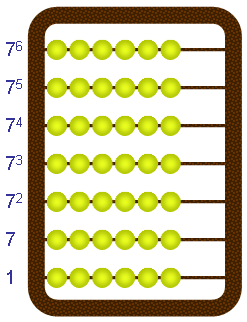
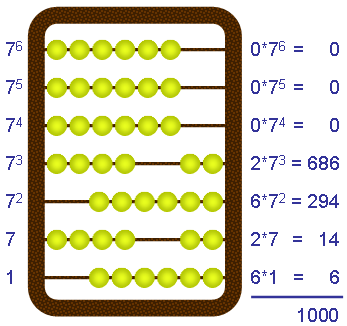
What is 1000 (base 10) on this abacus?

The factorial of a natural number is the product of all natural numbers equal or less than it… so 5 factorial = 5*4*3*2*1 = 120. The exclamation mark is the symbol used for factorial so 4! = 4*3*2*1 = 24. What would a factorial abacus look like? This is one idea:

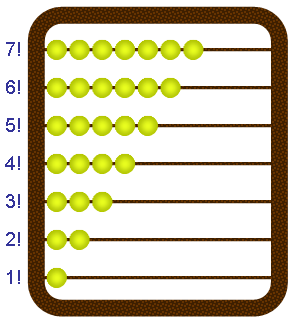
What is 1000 (base 10) on this abacus? Click here for the solution.

This abacus is difficult to use for most operations, but it does have some nice properties. For example, in order to check if a number is divisible by 2 what must be true? What about numbers divisible by 3? by 4? by 5? by 6? by 7?

History:

The most famous competition between the abacus and the calculator happened in 1946 in Tokyo, Japan. The abacus operator, Mr. Kiyoshi Matsuzaki, completed 50 additions of 3 to 6 digit numbers in 1 minute, 14 seconds as compared to 1 minute and 58 seconds by Pvt. Thomas Nathan Wood. At the end of the day the Nippon times reported: “Civilization, on the threshold of the atomic age, tottered Monday afternoon as the 2,000-year-old abacus beat the electric calculating machine in adding, subtracting, dividing… Only in multiplication alone did the machine triumph…”

Here is a base 10 abacus with the number 222:

Abacuses like the one above were never popular, maybe because they were too cumbersome for rapid calculations. The first popular abacus was the Suan-pan (below left) which originated about 1200 AD in China. The Soroban is a Japanese abacus that became popular in the 1930s and that Mr. Kiyoshi Matsuzaki probably used in the competition.

Extensions:

• Experiment using an abacus. Does the abacus help make you faster or more accurate when adding numbers? With practice, an abacus operator can add, subtract, multiply and divide quickly. At the start it may actually slow you down.
• Design your own abacus, or find other properties of existing abacuses.
• Why do the most common abacuses in the world look like the Suan-pan or the Soroban? Can you guess what the beads in the upper row are for?
• Slide the same number of beads on two different abacuses to produce the same number.
• Prove that any whole numbers less than 40,000 may be expressed in a unique way by the factorial abacus shown above.