Nano Hopscotch

In 1985 Nanotechnology guru, Richard Smalley, discovered the smallest soccer ball. It was made of 60 carbon atoms as shown on the right.

On October 28th, 2005, Richard Smalley suddenly began shrinking. He became so small that he could no longer be seen.

He had shrunk to the size of the carbon rings that he had studied. Not having anyone to talk with, Richard began playing a game with the carbon rings. First he snapped a few of them together to form the rhombus, then stepped into one of them as shown below.

Then he rolled a dice and jumped in the direction indicated… He did this again and again. If he ever made a roll that would make him move out of the rings or pointed towards a ring he had already visited – he would roll again.

For example, the first time he played, he started by rolling a 6 he could not move so he rerolled. He then rolled a 3 and still could not move so he rerolled again. Then he rolled a 1 and moved as shown:

He continued by rolling a 6:

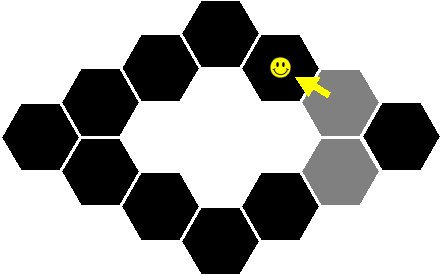
Richard then rolled a 3 which would have made him visit a ring which he had previously visited so he had to reroll… This game continued for about 5 minutes. Then he played again and again…

Richard wins if he visits all of the carbon rings in his rhombus.

• Is Richard sure to win no matter where he starts? If not, is there some carbon ring where Richard can start so that he is sure to win?
• Is Richard sure to lose no matter where he starts? If not, is there some carbon ring where Richard can start so that he is sure to lose?

Next, Richard snapped together 7 carbon rings to form a “flower”:

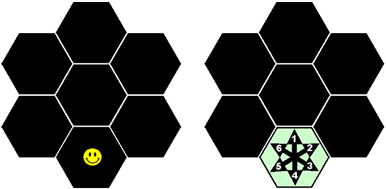
(For those of you working with the Galileo Math Box, instead of representing Richard by his happy face, you could represent him with the arrows as shown on the right.)

• Is Richard sure to win no matter where he starts? If not, is there some carbon ring where Richard can start so that he is sure to win?
• Is Richard sure to lose no matter where he starts? If not, is there some carbon ring where Richard can start so that he is sure to lose?

Extensions:

• Categorize the following ring shapes for Richard:

• Lucas and Casey-May of Alice M. Curtis Campus ask if the “9” and the “3” are possible to solve, and if they are possible, where can you start?

• Is it possible to snap together 7 rings to form a shape which is impossible to win from some starting positions, but always gives a win from other starting positions?
• Is it possible to snap together 7 rings to form a shape which always gives a win from any starting position?
• Is it possible to snap together 7 rings to form a shape which is impossible to win from any starting position?
• Is it possible to snap together 7 rings to form a shape which is possible to win from any starting position, but no starting position guarantees a win?
• Now answer all of these questions for all other positive integers.
• Richard has found that a repeating sequence of rolls {2,5,1,4} allows him to win on the shape on the left, but not on the shape on the right:

• Find a repeating sequence of four rolls that allows him to solve both shapes.
• Find a winning repeating sequence of length 3 for the triangle below and length 6 for the hexagon below. Are these the shortest possible repeating sequences?

• Choose any shape. Prove that it is winnable by a repeating sequence of length < L or prove that no such L exists.
• Snap together some rings to form a shape that is impossible to win from half its starting positions, but a guaranteed win from the other half of its starting positions.
• Is it possible to snap together some rings to form a shape that is impossible to win when starting at all but one special ring?
• Either prove that no shape exists in which the probability of winning from each ring is P where 0 < P < 1 or find a shape for which this is true. (We have not solved this.) If there does not exist such a shape, Let Q be the largest probability for any ring and P the smallest probability for any ring (0 < P < Q < 1). What is the shape with minimum Q/P? (We have not solved this.) At least find a shape where Q/P = 2.

Hint #1

• The probability of winning from a ring in some shape is P where 0 < P < 1. How high can P be? (We have not solved this.) If this is too difficult at least find a ring where P=3/4.

Hint #2

This problem is dedicated to the memory of the 1996 Nobel Laureate of Chemistry, Richard Smalley. The carbon “soccer ball” which Richard discovered in 1985 and named the Bucky-ball after Buckminster. Here Richard is seen through a carbon tube that he called the Bucky-Tube.