Galileo Educational Network – Inspiring a Passionate Commitment to Learning
Category: 3D Objects & 2D Shapes, Variables & Equations, Relations & Functions, and Patterns
Suitable for Grade Level: Elementary and Secondary
The Math in this Problem:
This is a classic problem, also known as the Seven Bridges of Kӧnigsberg, which was solved by Leonhard Euler, one of the greatest mathematicians. Party in Kӧnigsberg challenges students to analyze the vertices, edges, and faces of proposed surfaces and derive a solution to this topology problem similar to that of the Euler characteristic.
If you are already familiar with The Bridges of Konigsberg, please proceed to The Party in Konigsberg.
The Bridges of Konigsberg:
In the eighteenth century, one of the most brilliant mathematicians, Euler, was in Konigsberg. The river Pregel divided the town into four separate districts, A, B, C, and D and seven bridges connected these districts. In the summertime, the citizens of Konigsberg often went for walks around their city, and so the famous question was posed to Euler: “Is it possible to go over all the bridges in our town once and only once?”
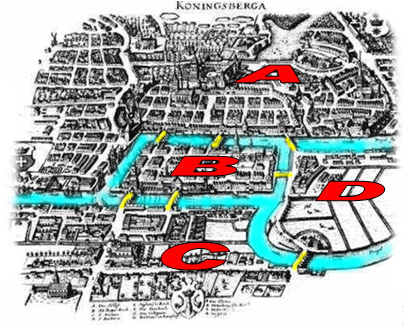
Dealing with city maps can be messy, so Euler first “cleaned-up” the problem (Mathematicians are always cleaning up problems so that they can focus on what is important.)
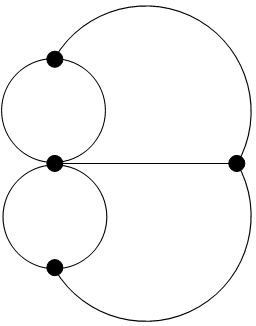
The cleaned up question became: “Is it possible to draw the 4-point, 7-line graph above if you are only permitted to trace each line once?” Can you see why this question is equivalent to the original?
Euler presented his solution in 1735 at the Russian Academy of Science. Can you reconstruct Euler’s solution?
The Party in Konigsberg:
After the solution was made known to Euler’s friends in Konigsberg, they went to their favourite restaurant to party. After the meal was finished they all walked home, and were later thrilled to discover that they had collectively crossed each bridge once and only once. How many friends might Euler have in Konigsberg and which districts could they have eaten in?
Extensions:
- Where could the people of Konigsberg build a bridge to change the answers?
- Which bridge could they remove to change the answers?
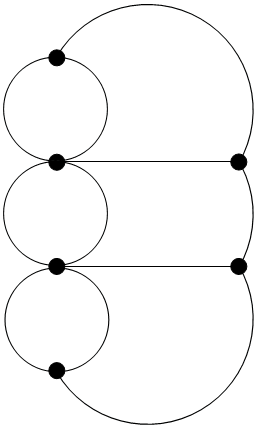
- The bridges of Eulerberg are shown above. If Euler’s friends in Eulerberg were to party like those in Konigsberg, how many friends might Euler have had in Eulerberg and what districts could they have eaten in?
- Create a town where Euler’s friends could not party appropriately. What is the smallest such town? Create a town where Euler’s friends could party, but only in one district.
- Could Annie Ant have one of these Euler parties on her cube?
Credits: The Bridges of Konigsberg is a classic problem from one of the greatest mathematicians, Euler.