Menu Close

House of Gloom

Download PDF

Category: 3D Objects & 2D Shapes, Patterns, Measurements, Variables & Equations, Transformations, and Relations & Functions
Suitable for Grade Level: Elementary and Secondary

The Math in this Problem:

This math puzzle explores lines and angles, while working with different two-dimensional shapes and patterns. Students will incorporate their understanding of lines and angles with the practical application of experimenting with the effectiveness of lights in various surroundings.

In the valley in the heart of the dark wood lives a gloomy elf. His doorless home is painted totally black so dark that no light that touches a wall bounces back. However the gloomy elf lights part of his home with a firefly.

Floor plan of the House of Gloom

One day the gloomy elf awakes and decides that life is too short to always be gloomy. He decides to build another house. The new house will have only 12 black walls, but this time he wants to light it all! Find a design where the elf will need 4 fireflies.

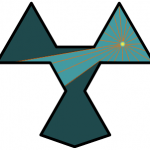
Example

The elf first thought he could make a giant G out of 12 walls. He thought it would take 4 fireflys as he shows on the left, but the design actually only needs three fireflys so the G is not a solution.

Hint #1

One way to proceed when you get stuck with a problem, is to look at simpler problems that are related.

Convince yourself that at most one firefly is required to totally illuminate houses with 3, 4, and 5 walls:

  • Find an example for a 6 walled house that requires 2 fireflies.
  • Next try to find a 9 walled house that requires 3 fireflies.
  • Now go back and try to find a 12 walled house that requires 4 fireflies.
  • You might even find a pattern for a 3N walled house requiring N fireflies.

Extensions:

  • Find a floor pattern with W walls where W/3 (rounded down) fireflies are required.
  • If all 12 wall segments must be the same length, is it still true that 4 fireflies may be needed to light the house?
Hint #2
Seven fireflies are needed to light this house of 21 walls.

  • Prove that the formerly gloomy elf needs no more than W/3 (rounded down) fireflies if he builds W walls (difficult).
  • Find a design using 7 walls where 3 fireflies can hide without seeing each other. Find a design using less walls and more fireflies for which this is true.
  • At the top of a mountain overlooking the valley of the once gloomy elf, lives his cousin in a house of mirrors. Is it possible that a single firefly can light the whole house no matter how many walls it has?

Warning: This extension is an unsolved problem in mathematics.