Galileo Educational Network – Inspiring a Passionate Commitment to Learning
Category: Variables & Equations, Number Operations, and Patterns
Suitable for Grade Level: Elementary and Secondary
The Math in this Problem:
Game theory is a form of mathematics, which attempts to predict behaviour in any sort of strategic setting. This puzzle involves careful tactical patterns and analytical processing in order to master this math challenge. Similar to other strategy-based games, Frog Catchers is concerned with the evaluation of setting up goals and future play possibilities of one’s opponent.
This is a game for two frog catchers.
There are a bunch of frogs to catch and one special frog. You and a friend are frog catchers and each of you wants to catch THE special frog. You take turns. At each turn you can catch one or two frogs. To catch THE special frog, it must be THE last frog, or one of THE last two frogs that are caught. Can you figure out a strategy to win?
Extensions:
- Try it with six frogs plus the special frog:
- What if the frogs in the outer circle could only be caught together if they were side-by-side? For example the capture of the orange circled frogs is permitted, but not the capture of the red circled frogs:
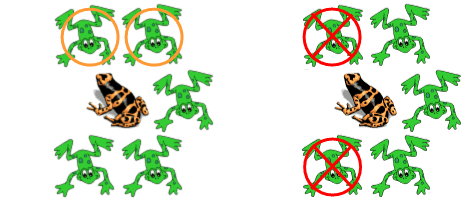
- If the special frog is poisonous, and you want to let your friend capture it, how would you play differently?
- Using both of these extensions, who wins if both players play well? The first player or the second player?
- Try the game with a different number of frogs.
