Galileo Educational Network – Inspiring a Passionate Commitment to Learning
Category: 3D Objects & 2D Shapes, Patterns, and Transformations
Suitable for Grade Level: Elementary
The Math in this Problem:
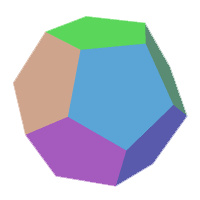
This math problem was invented by the great Irish mathematician, William Rowan Hamilton. In this Icosian game, the goal for students is to find a path such that every point is visited a single time and the ending point is the same as the starting point. This path is also known as the Hamiltonian cycle along the edges of a dodecahedron.
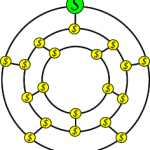
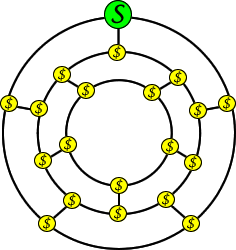
Sally is a sleepwalker. Each night she gets up without knowing it, puts on her slippers and coat, and wanders around her village for an hour or so, then returns home, climbs upstairs, and gets into bed. The only reason Sally knows she sleepwalks is because her coat has a hole in its pocket so she drops things as she sleepwalks.
One day Sally sleepwalked with her coat pocket full with pennies. When she woke up in the morning and walked around her village, she found a penny at each intersection. When she had picked up all the pennies and returned home she suddenly realized something interesting… she had not walked on any street more than once! How did she do it?
Extensions:
- Sally can choose her first street to walk down in 3 ways. Her second, third and fourth choices are between two streets. Can Sally pick up all her pennies no matter which decisions she has made?
- How is Sally’s problem similar to an edge-travelling alien picking corner-growing tomatoes on her dodecahedral asteroid?
